Introduction
Binary search is a searching algorithm for finding items in a sorted sequence of items. Many individuals utilize binary search without even realizing it.
For example, let’s find a word in the dictionary that starts with the letter R. First, open the dictionary in the middle and check which letter the words start with. If the start letter is located before R in alphabetic order, the half from the current position to the end of the dictionary is opened or the other half from the beginning position to the current position is opened. Repeat these steps until the words start with the letter R.
Another example of using binary search is finding a chapter in a book. If necessary to find chapter number 8, open a book in the middle and check the chapter number on the page. If the chapter number is less than 8, the second half of the book opens, otherwise the first half opens. This algorithm works much faster than searching page by page from the beginning of a book to its end (linear search).
General algorithm
In computer science, binary search is used to find a target element in a sorted array. Using examples can describe the general binary search algorithm. Consider an array
- Set
\(L\) to\(0\) and\(R\) to\(n\ – 1\) .\(L\) and\(R\) to indicate the left and right boundaries of the array for searching. - If
\(L > R\) , the search terminates as unsuccessful. - Set
\(m\) to the floor of\((L + R) / 2\) .\(m\) is the position of the middle element. - If
\(A_m < T\) , set\(L\) to\(m + 1\) and go to step 2. - If \(A_m > T\), set
\(R\) to\(m\ – 1\) and go to step 2. - If
\(Am = T\) , the search is done.\(m\) contains the index of the searched element.
This algorithm can be implemented using a recursion or iterative approach.
Approximate matches
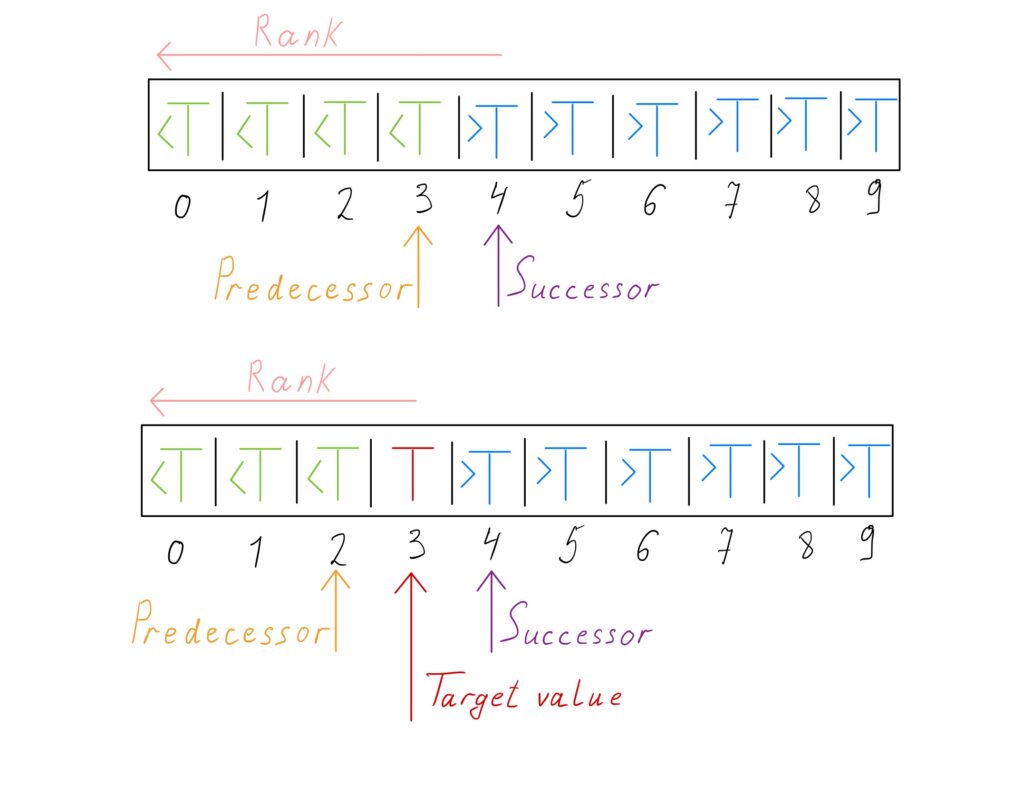
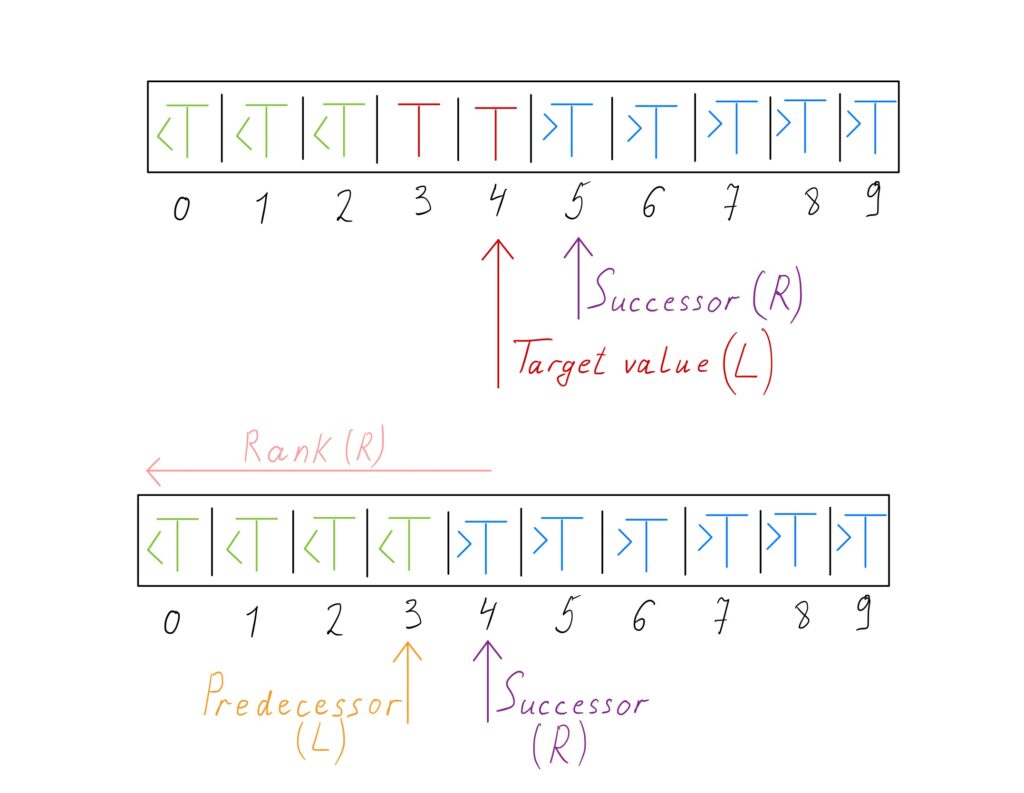
The described general algorithm only performs exact matches, finding the position of a target value. However, binary search could be extended to perform approximate matches because binary search operates on sorted arrays. Binary search is used to find:
- Target value.
- Rank. It is the number of smaller elements. Rank queries can be performed with the implementation for finding the leftmost element.
- Predecessor. It is the next smallest element after the target element. Predecessor queries can be performed with rank queries. If the rank of the target value is \(r\), its predecessor is \(r\ – 1\).
- Successor. It is the next largest element after the target element. For successor queries, the implementation for finding the rightmost element can be used. If the result of running the implementation for the target value is \(r\), then the successor of the target value is \(r\ + 1\).
- Nearest neighbor. It is the successor or predecessor of the target element, which is closer.
Time and Space complexity
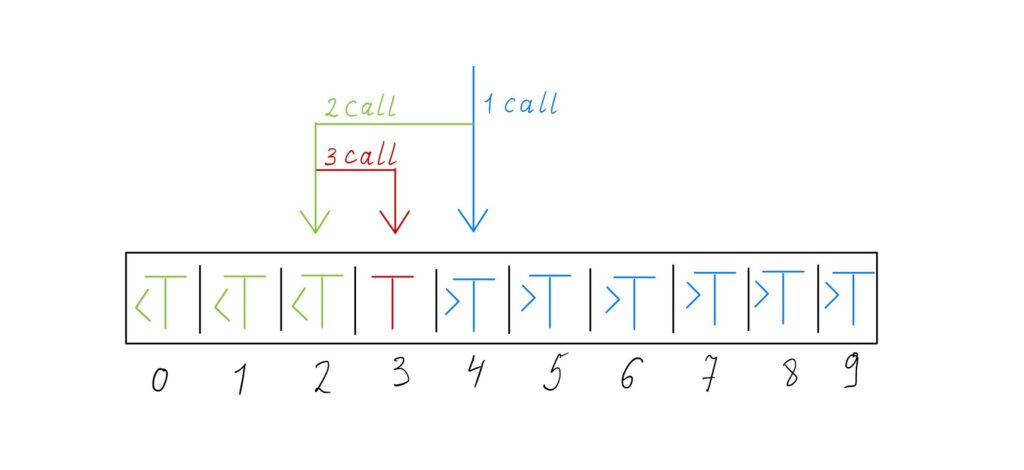
The described algorithm can relate to the divide and conquer approach because each search performs one comparison with the target element and the search space is divided into two equal parts. Search continues from one of them.
Perform a binary search on an array of size
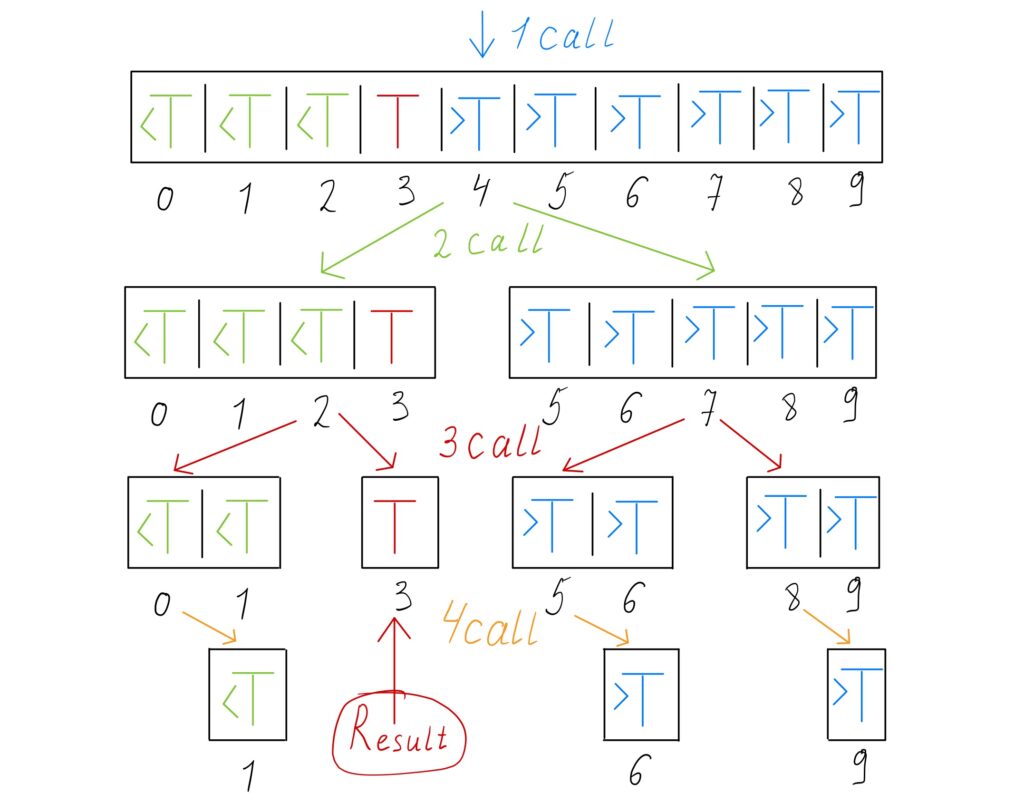
At comparison \(k\), the algorithm will search in the array of size at most \(n / (2^k)\). The search is terminated when there is no subarray for further search. The size of the array at the last comparison equals \(1.\) Complexity of the algorithm equals the total number of comparisons that is the smallest
Another way to estimate complexity is to use the master theorem for divide and conquer recurrences:
The size of input
So, the average time complexity of binary search is
In the best case, the target element will be in the middle of the initial array. One comparison is required to find it. So best case time complexity is
In the worst case will be performed
The iterative approach of binary search uses additional space for two variables
The recursive approach of binary search uses no additional space for input, but there will be a k recursive calls stored in memory, one call for each comparison, so space complexity is
| Average performance | |
| Worst-case performance | |
| Best-case performance | |
| Worst-case space complexity (Iterative) | |
| Worst-case space complexity (Recursive) |
Implementations
There are many implementations of binary search that can be written. I will consider 5 variants of binary search implementations. These implementations do not have commonly accepted names, so I have named them according to the result of their work.
In different implementations, the middle position can be calculated using the function floor or ceil. An example of using the ceil will be shown in the rightmost implementation of binary search.
In programming languages with strong typing, the computation position of the middle element can lead to overflow. This can be avoided by calculating the floor of the middle position as
Exact match
The result of the exact match implementation is the index of the first element in the sorted array, which is equal to the target element. If the target element does not exist in the array, the function reports the absence of the element. This implementation follows the general algorithm step by step. It can be implemented using a recursive or iterative approach.
For the remaining variants of the implementation, only the iterative implementation will be shown since it has no recursive call overhead.
Recursive approach
C++
#include <iostream>
#include <vector>
size_t FirstMatchBinarySearch(int T, size_t L, size_t R,
const std::vector<int>& A) {
if (L > R)
return A.size();
size_t m = L + (R - L) / 2;
if (A[m] < T) {
return FirstMatchBinarySearch(T, m + 1, R, A);
} else if (A[m] > T) {
return FirstMatchBinarySearch(T, L, m - 1, A);
} else {
return m;
}
return A.size();
}
int main() {
std::vector<int> A { 1, 3, 5, 6, 7, 9 };
std::cout << FirstMatchBinarySearch(9, 0, A.size() - 1, A) << std::endl;
std::cout << FirstMatchBinarySearch(2, 0, A.size() - 1, A) << std::endl;
return 0;
}Output:
5
6Python
def FirstMatchBinarySearch(T, L, R, A):
if (L > R):
return len(A)
m = (R + L) // 2
if (A[m] < T):
return FirstMatchBinarySearch(T, m + 1, R, A)
elif (A[m] > T):
return FirstMatchBinarySearch(T, L, m - 1, A)
else:
return m
return len(A)
A = [ 1, 3, 5, 6, 7, 9 ];
print(FirstMatchBinarySearch(9, 0, len(A) - 1, A))
print(FirstMatchBinarySearch(2, 0, len(A) - 1, A))Output:
5
6Iterative approach
C++
#include <iostream>
#include <vector>
size_t FirstMatchBinarySearch(int T, const std::vector<int>& A) {
size_t L = 0;
size_t R = A.size() - 1;
size_t m;
while (L <= R) {
m = L + (R - L) / 2;
if (A[m] < T) {
L = m + 1;
} else if (A[m] > T) {
R = m - 1;
} else {
return m;
}
}
return A.size();
}
int main() {
std::vector<int> A { 1, 3, 5, 6, 7, 9 };
std::cout << FirstMatchBinarySearch(9, A) << std::endl;
std::cout << FirstMatchBinarySearch(2, A) << std::endl;
return 0;
}Output:
5
6Python
def FirstMatchBinarySearch(T, A):
L = 0
R = len(A)
while (L <= R):
m = (R + L) // 2
if (A[m] < T):
L = m + 1
elif (A[m] > T):
R = m - 1
else:
return m
return len(A)
A = [ 1, 3, 5, 6, 7, 9 ];
print(FirstMatchBinarySearch(9, A))
print(FirstMatchBinarySearch(2, A))Output:
5
6Leftmost element
If the array contains duplicate elements, the previous implementation returns the first element that matches the target element, which may not be equal to the leftmost or rightmost element. However, it is sometimes necessary to find the leftmost element or the rightmost element for a target value that is duplicated in the array. This implementation will always return the leftmost element if such an element exists.
- Set
\(L\) to\(0\) and\(R\) to\(n\) . - While
\(L < R\) ,
- Set Set \(m\) to the floor of \((L + R) / 2\).
- If
\(A_m < T\) , set\(L\) to\(m + 1\) . - Else \(A_m \ge T\), set
\(R\) to\(m\) .
- Return
\(L\) .
If
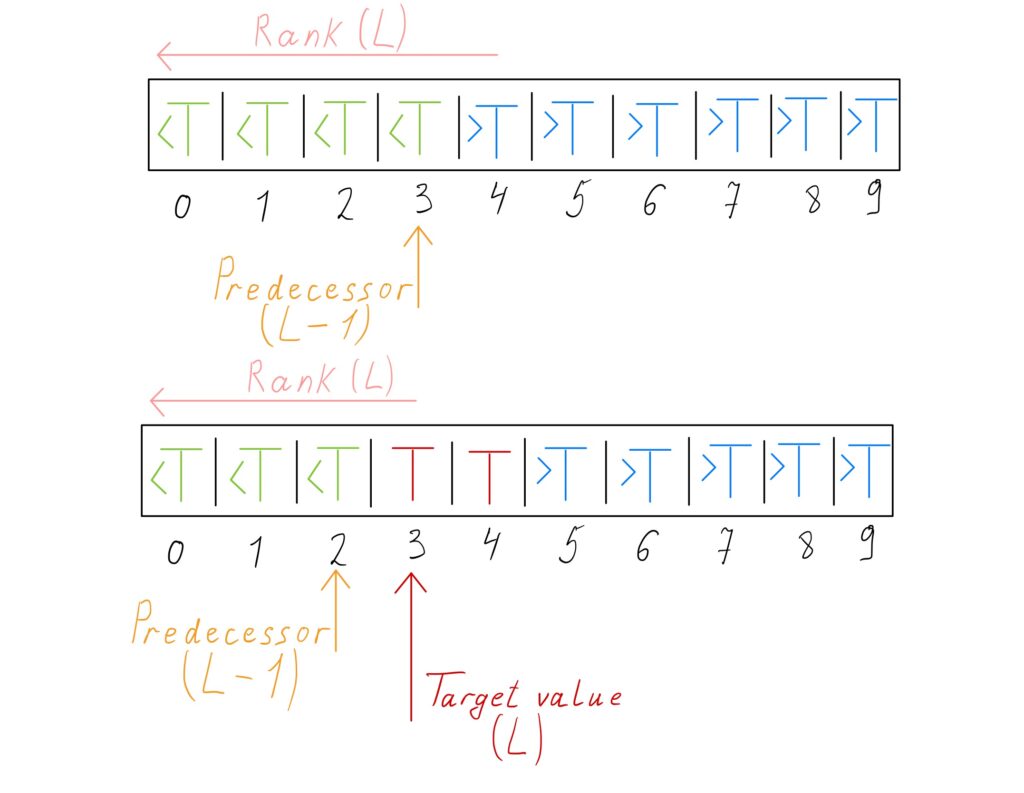
Since the pointers converge on the same element, the values of \(L\) and \(R\) are the same at the end of the algorithm.
C++
#include <iostream>
#include <vector>
size_t LeftmostBinarySearch(int T, const std::vector<int>& A) {
size_t L = 0;
size_t R = A.size();
size_t m;
while (L < R) {
m = L + (R - L) / 2;
if (A[m] < T) {
L = m + 1;
} else {
R = m;
}
}
return L;
}
int main() {
std::vector<int> A { 1, 3, 5, 6, 7, 7, 7, 7, 9 };
std::cout << LeftmostBinarySearch(7, A) << std::endl;
std::cout << LeftmostBinarySearch(1, A) << std::endl;
std::cout << LeftmostBinarySearch(2, A) << std::endl;
std::cout << LeftmostBinarySearch(-1, A) << std::endl;
std::cout << LeftmostBinarySearch(10, A) << std::endl;
return 0;
}Output:
4
0
1
0
9Python
def LeftmostBinarySearch(T, A):
L = 0
R = len(A)
while (L < R):
m = (R + L) // 2
if (A[m] < T):
L = m + 1
else:
R = m
return L
A = [ 1, 3, 5, 6, 7, 7, 7, 7, 9 ];
print(LeftmostBinarySearch(7, A))
print(LeftmostBinarySearch(1, A))
print(LeftmostBinarySearch(2, A))
print(LeftmostBinarySearch(-1, A))
print(LeftmostBinarySearch(10, A))Output:
4
0
1
0
9Rightmost element
Implementation for finding the rightmost element that has duplicates in the sorted array, if such an element exists.
- Set
\(L\) to\(0\) and\(R\) to\(n\) . - While
\(L < R\) ,
- Set Set \(m\) to the floor of \((L + R) / 2\).
- If
\(A_m > T\) , set\(R\) to\(m\) . - Else \(A_m \le T\), set
\(L\) to\(m + 1\) .
- Return
\(R\) .
If
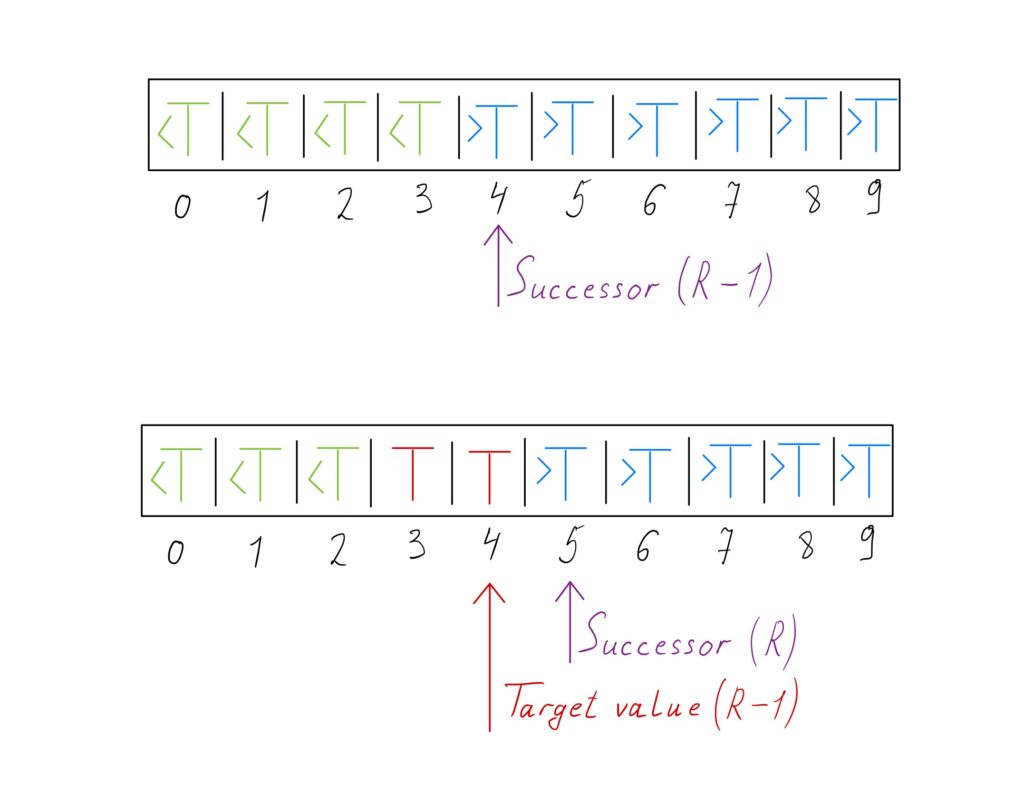
Since the pointers converge on the same element, the values of \(L\) and \(R\) are the same at the end of the algorithm.
C++
#include <iostream>
#include <vector>
size_t RightmostBinarySearch(int T, const std::vector<int>& A) {
size_t L = 0;
size_t R = A.size();
size_t m;
while (L < R) {
m = L + (R - L) / 2;
if (A[m] > T) {
R = m;
} else {
L = m + 1;
}
}
return R;
}
int main() {
std::vector<int> A { 1, 3, 5, 6, 7, 7, 7, 7, 9 };
std::cout << RightmostBinarySearch(7, A) << std::endl;
std::cout << RightmostBinarySearch(1, A) << std::endl;
std::cout << RightmostBinarySearch(2, A) << std::endl;
std::cout << RightmostBinarySearch(-1, A) << std::endl;
std::cout << RightmostBinarySearch(10, A) << std::endl;
return 0;
}Output:
8
1
1
0
9Python
def RightmostBinarySearch(T, A):
L = 0
R = len(A)
while (L < R):
m = (R + L) // 2
if (A[m] > T):
R = m
else:
L = m + 1
return R
A = [ 1, 3, 5, 6, 7, 7, 7, 7, 9 ];
print(RightmostBinarySearch(7, A))
print(RightmostBinarySearch(1, A))
print(RightmostBinarySearch(2, A))
print(RightmostBinarySearch(-1, A))
print(RightmostBinarySearch(10, A))Output:
8
1
1
0
9This algorithm can be modified to reduce the post-execution checks to a single check
- Set
\(L\) to\(0\) and\(R\) to\(n\ – 1\) . - While
\(L < R\) ,
- Set Set \(m\) to the ceil of \((L + R) / 2\).
- If
\(A_m > T\) , set\(R\) to\(m\ – 1\) . - Else \(A_m \le T\), set
\(L\) to\(m\) .
- Return
\(R\) .
If \(A_R = T\), then \(A_R\) is the rightmost element that equals \(T\).
C++
#include <iostream>
#include <vector>
size_t RightmostBinarySearch(int T, const std::vector<int>& A) {
size_t L = 0;
size_t R = A.size() - 1;
size_t m;
while (L < R) {
m = R - (R - L) / 2;
if (A[m] > T) {
R = m - 1;
} else {
L = m;
}
}
return R;
}
int main() {
std::vector<int> A { 1, 3, 5, 6, 7, 7, 7, 7, 9 };
std::cout << RightmostBinarySearch(7, A) << std::endl;
std::cout << RightmostBinarySearch(1, A) << std::endl;
std::cout << RightmostBinarySearch(2, A) << std::endl;
std::cout << RightmostBinarySearch(-1, A) << std::endl;
std::cout << RightmostBinarySearch(10, A) << std::endl;
return 0;
}Output:
7
0
0
0
8Python
def RightmostBinarySearch(T, A):
L = 0
R = len(A) - 1
while (L < R):
m = (R + L + 1) // 2
if (A[m] > T):
R = m - 1
else:
L = m
return R
A = [ 1, 3, 5, 6, 7, 7, 7, 7, 9 ];
print(RightmostBinarySearch(7, A))
print(RightmostBinarySearch(1, A))
print(RightmostBinarySearch(2, A))
print(RightmostBinarySearch(-1, A))
print(RightmostBinarySearch(10, A))Output:
7
0
0
0
8Leftmost or smaller and larger element
In this implementation, if the target element does not exist in the array, one pointer holds the position of the element that is smaller than the target element, and the other pointer holds the position of the element that is larger than the target element. If the target element exists in the array then one of them holds the position of the target element. If the target element has duplicates, then another pointer may hold the position of the duplicated target element.
- Set
\(L\) to\(0\) and\(R\) to\(n\) . - While
\(L < R\ – 1\) ,
- Set Set \(m\) to the floor of \((L + R) / 2\).
- If
\(A_m < T\) , set\(L\) to\(m\) . - Else \(A_m \ge T\), set
\(R\) to\(m\) .
- Return
\(L\) and\(R\) .
If
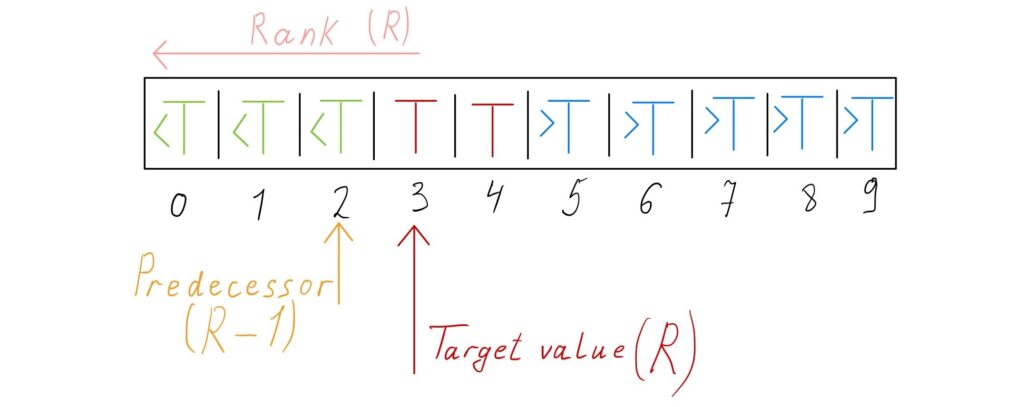
If \(A_L = T\), then \(A_L\) is the leftmost element that equals \(T\). \(R\) is the position of element that is larger than \(T\) if
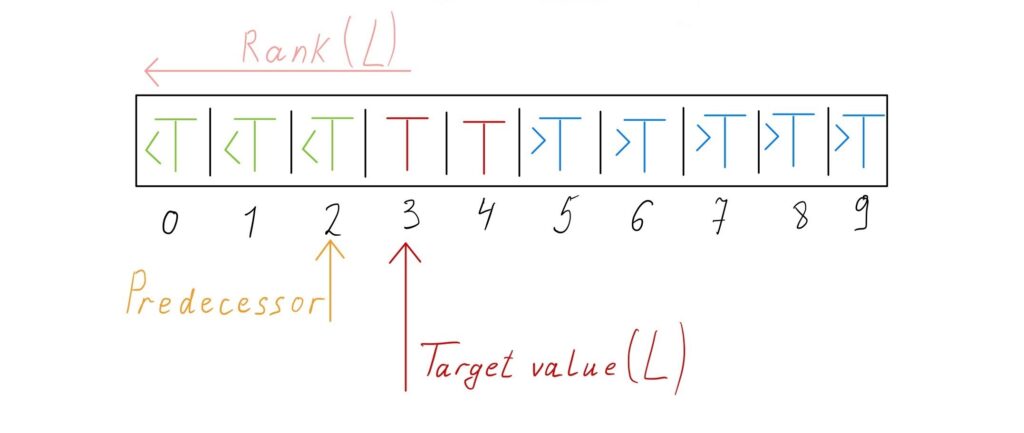
If \(T\) is not in the array, \(R\) is the position of the element larger than \(T\) and \(L\) is the position of the element that is smaller than \(T\).
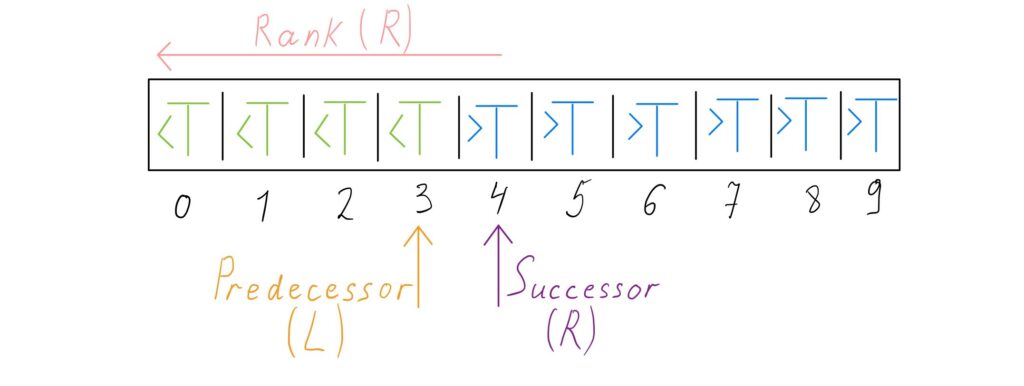
C++
#include <iostream>
#include <vector>
struct Result {
size_t L, R;
};
Result LeftmostSmallerLargerBinarySearch(int T, const std::vector<int>& A) {
size_t L = 0;
size_t R = A.size();
size_t m;
while (L < R - 1) {
m = L + (R - L) / 2;
if (A[m] < T) {
L = m;
} else {
R = m;
}
}
return (Result { L, R });
}
int main() {
std::vector<int> A { 1, 3, 5, 6, 7, 7, 7, 7, 9 };
Result result;
result = LeftmostSmallerLargerBinarySearch(7, A);
std::cout << result.L << ' ' << result.R << std::endl;
result = LeftmostSmallerLargerBinarySearch(1, A);
std::cout << result.L << ' ' << result.R << std::endl;
result = LeftmostSmallerLargerBinarySearch(2, A);
std::cout << result.L << ' ' << result.R << std::endl;
result = LeftmostSmallerLargerBinarySearch(-1, A);
std::cout << result.L << ' ' << result.R << std::endl;
result = LeftmostSmallerLargerBinarySearch(10, A);
std::cout << result.L << ' ' << result.R << std::endl;
return 0;
}Output:
3 4
0 1
0 1
0 1
8 9Python
def LeftmostSmallerLargerBinarySearch(T, A):
L = 0
R = len(A)
while (L < R - 1):
m = (R + L) // 2
if (A[m] < T):
L = m
else:
R = m
return L, R
A = [ 1, 3, 5, 6, 7, 7, 7, 7, 9 ];
print(LeftmostSmallerLargerBinarySearch(7, A))
print(LeftmostSmallerLargerBinarySearch(1, A))
print(LeftmostSmallerLargerBinarySearch(2, A))
print(LeftmostSmallerLargerBinarySearch(-1, A))
print(LeftmostSmallerLargerBinarySearch(10, A))Output:
(3, 4)
(0, 1)
(0, 1)
(0, 1)
(8, 9)Rightmost and smaller or larger element
In this implementation, one pointer holds the position of the rightmost element. If such an element does not exist then that pointer holds the position of the element that is smaller than the target element. The other pointer holds the position of the element that is larger than the target element if the target element has no duplicates.
- Set
\(L\) to\(0\) and\(R\) to\(n\) . - While
\(L < R\ – 1\) ,
- Set Set \(m\) to the floor of \((L + R) / 2\).
- If
\(A_m > T\) , set\(R\) to\(m\) . - Else \(A_m \le T\), set
\(L\) to\(m\) .
- Return
\(L\) and\(R\) .
If \(A_L = T\), then \(A_L\) is the rightmost element that equals \(T\). \(R\) is the position of element that is larger than \(T\) if \(A_R \ne T\). If \(T\) is not in the array, \(L\) is the position of the element that is smaller than \(T\).
C++
#include <iostream>
#include <vector>
struct Result {
size_t L, R;
};
Result RightmostSmallerLargerBinarySearch(int T, const std::vector<int>& A) {
size_t L = 0;
size_t R = A.size();
size_t m;
while (L < R - 1) {
m = L + (R - L) / 2;
if (A[m] > T) {
R = m;
} else {
L = m;
}
}
return (Result { L, R });
}
int main() {
std::vector<int> A { 1, 3, 5, 6, 7, 7, 7, 7, 9 };
Result result;
result = RightmostSmallerLargerBinarySearch(7, A);
std::cout << result.L << ' ' << result.R << std::endl;
result = RightmostSmallerLargerBinarySearch(1, A);
std::cout << result.L << ' ' << result.R << std::endl;
result = RightmostSmallerLargerBinarySearch(2, A);
std::cout << result.L << ' ' << result.R << std::endl;
result = RightmostSmallerLargerBinarySearch(-1, A);
std::cout << result.L << ' ' << result.R << std::endl;
result = RightmostSmallerLargerBinarySearch(10, A);
std::cout << result.L << ' ' << result.R << std::endl;
return 0;
}Output:
7 8
0 1
0 1
0 1
8 9Python
def RightmostSmallerLargerBinarySearch(T, A):
L = 0
R = len(A)
while (L < R - 1):
m = (R + L) // 2
if (A[m] > T):
R = m
else:
L = m
return L, R
A = [ 1, 3, 5, 6, 7, 7, 7, 7, 9 ];
print(RightmostSmallerLargerBinarySearch(7, A))
print(RightmostSmallerLargerBinarySearch(1, A))
print(RightmostSmallerLargerBinarySearch(2, A))
print(RightmostSmallerLargerBinarySearch(-1, A))
print(RightmostSmallerLargerBinarySearch(10, A))Output:
(7, 8)
(0, 1)
(0, 1)
(0, 1)
(8, 9)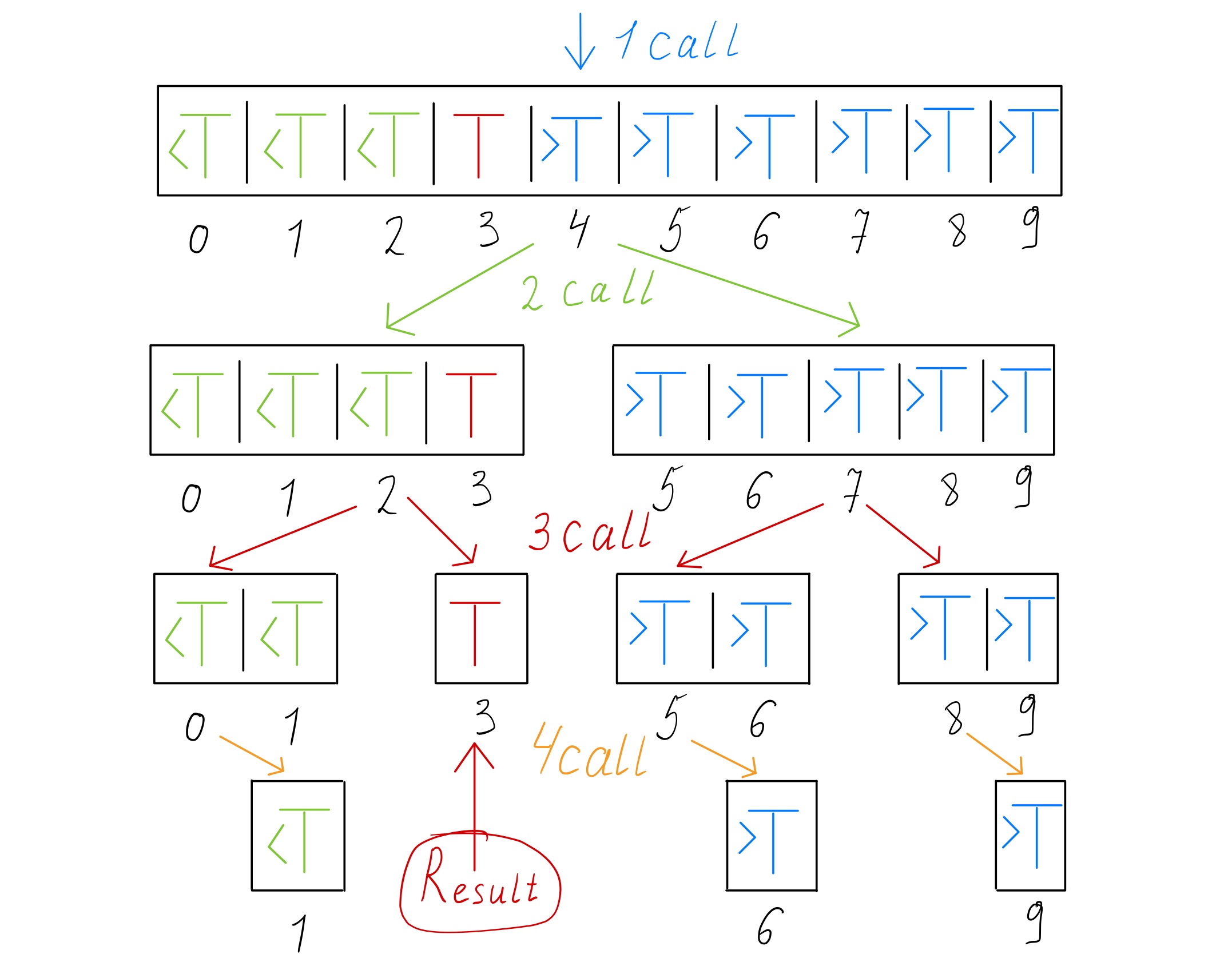
Be First to Comment